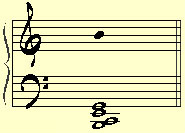⊙ 음악(音樂, music) : 어원적으로는 '예술적으로나 오락적으로 음을 즐긴다'는 것이지만 학구적으로는 「음의 움직임을 잘 조정하는 지식」이라고 정의된다. 세부적으로는 장르적으로, 역사와 시대적으로, 학술적으로, 종교나 국가간의 관념적으로, 표현양식으로 분류될 수 있지만 궁극적으로는 「귀를 위한 울림이 어떠한 질서를 가지고 움직이는 형식」으로 결론 지을 수 있다.
⊙ 음악의 요소 : 음악을 구성하는 요소는 기본적으로 리듬(rhythm), 선율(melody), 화성(harmony)이지만 근대 이후로 음색(timber)까지 음악의 요소로서 취급되는 경우가 많다.
⊙ 실용음악(實用音樂, Gebrauchsmusik [獨] - 게우라우흐스무지크) : 「힌데미트」등에 의해 제창된 용어로서 본래는 전문적(음악 그 자체, 즉 예술을 위한 예술로서 작곡된 음악) 음악과 대립되는 아마추어적이고 가벼운 음악 개념의 용어로 쓰여졌지만 최근에는 각 음악장르가 파괴되고 혼재되는 양상 속에서 장르의 구분 없이 상업적이고 대중적인 음악으로 확대되어 쓰여진다.
배 음(overtone)
바탕음(基音)의 진동수에 대해 정수배의 진동수를 갖는 상음(上音)을 말하며 사인파(sine wave)를 제외한 모든 소리는 배음을 가지고 있다. 즉 어떤 자연음도 그 음향 속에는 다음의 구조와 같은 자연 배음(natural overtone)을 포함하고 있다.
※ 이러한 배음의 현상은 음정의 협화관계나 화성현상의 기초로서, 또한 음향 구조의 안정적 관계 - 음 빛깔(tone colour)이나 음향으로서의 음색(timber)을 결정 짓는 등- 에 이르기까지 중요하게 응용된다.
- 짜임새에 있어서의 조밀도는 밑에서 얇고 위에서 두껍다. 이것을 음향적으로 응용하면 수직적 울림을 안정적으로 균형 있게 한다.
- 강한 근음진행(root motion)이 아래에서 나타난다. 이를 「근음강세」라고 하는데 근음강세는 협화(comsonance)와 불협화(dissonance)와 비례하여 배음열의 상향순서에 따른다.
증4도(감5도) 음은 3온음(tritone)으로서 옥타브의 중간에 해당하며 음악 양식이나 맥락에 따라 협화와 불협화로 구분하는 애매한 중성적(neither) 음정이다. 즉 무조적 현대음악에서는 협화로 취급되나 전통적 조성음악에서는 불협화로 간주된다. 완전4도 음정도 전통적 2성대위법에서는 불협화로 간주되었지만 9~16세기의 오르가늄(organum)양식 -다성음악(polyphony)의 초기 형태로서 4, 5도 병진행 서법- 에서는 협화음정으로 여겼다.
이러한 근음강세는 화성분석이나 청음(聽音, music dictation)을 용이하게 한다. 그 방법은 화음 가운데 강한 음정강세(위의 악보 참조)를 가지는 음정을 우선 추출하여 홀수 음정(3,5,7)은 아랫쪽이 그 화음의 근음(root)이 되고 짝수 음정(2,4,6)은 음정의 윗 음이 그 화음의 근음이 된다. (옥타브 이상의 겹음정은 옥타브 이내로 전위하여 계산하고 다시 원위치 한다)
- 배음열에서 제 6배음까지가 장3화음을 구성하고 있음을 알 수 있다.
- 배음열 구조는 다음과 같은 방법으로 그 가운데 어느 한 음을 활성화시킬 수 있다.
먼저 피아노의 패달을 밟지 않고 낮은 쪽 건반에서 몇 개의 음을 약하게 누르고 밑에서 눌렀던 음들의 배음구조 안에 있는 어떤 음(임의의 음이라도 좋다.)을 약간 세게 친다. 건반에서 손을 뗀 뒤 댐퍼 패달을 밟았다가 떼었을 때 피아노 내부의 현은 멈추었을지라도 배음 관계를 가지는 음이 잔향으로서 남게 되는데 이러한 현상을 「공명」(resonance) -어떤 발음체의 진동 에너지를 다른 것이 흡수하여 함께 울리는 현상- 이라고 한다.
참고로 자연 배음열인 위의 장선법에 의한 상위 배음열에는 단3화음이 발생하지 않는다. 이에 대하여 화성적 이원론 에 의한 상음으로서의 배음열(Ober tonreihe)의 역정수배(逆整數倍)의 배음으로서, 바탕음에 대하여 아래쪽에 위치하는 배음렬(하위 배음열-Untertonreihe)을 상정하여 그것을 단화음의 근거로 했다.
그러나 이것은 어디까지나 이론상의 논리로서 자연 배음과는 무관한 것이다. 다음은 하위 배음열이다.
이원론(dualistic theory)
장 단조나 장 단화음이 어느 것이 우위에 있는 것이 아닌 기본적으로 이원적인 속성을 가지고 있다는 이론, 즉 단3화음은 장3화음의 반전에서 성립된다는 견해이다. 이원론은 16세기의 이탈리아의 음악 이론가 짜를리노의 이론에서 유래하며 그것은 18세기 프랑스의 라모의 이론의 바탕을 이루고 있으며 20세기 초 독일의 음악학자 리만(Hugo Riemann)에 의해 완성되었다.
음률(音律 : Temperament)
음률이란 음악에서 사용하는 음 높이의 상호관계를 음악적, 수학적으로 확정한 것을 말하며 이에 따라 악기의 음높이를 정하는 것을 조율(tuning- 서양음악의 오케스트라는 오보에(Oboe)의 「A」 음을 조율의 기본음으로 삼고 국악에서는 대금의 「임종, 林鐘」음(G음)을 조율의 기본음으로 삼는다)이라고 한다. 음률은 음의 진동수 그 자체가 아니라 진동수에 의한 비율을 말하는 것이며 현재의 평균율(temperament) 외에도 고대(B.C 54년 경)로부터의 피타고라스 음계(Pythagoras scale)를 포함하는 순정율, 동양에서는 B.C 8~5세기 경의 삼분손익율(三分損益律)>)등이 있다.
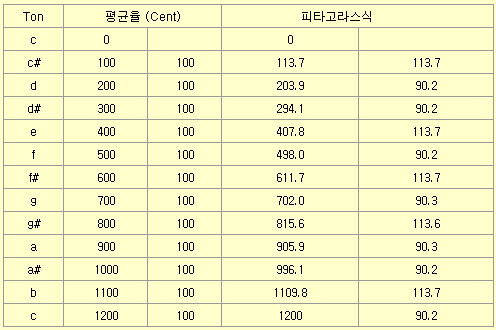
음율은 앞서의 자연 배음과도 무관치 않은 것으로서 진동수비 2:1은 8도, 3:2는 5도, 4:3은 4도라는 자연 음향의 원칙이 고대로부터 수학적인 논리와 결합되어 생성된 것이다. 이들은 순수한 자연의 울림이라는 차원에서의 장점은 있지만 필연적으로 균등하지 못한 반음관계로 인하여 조바꿈이 어렵고 성악과 기악간의 불균형이 초래는 등 불편한 점 때문에 19세기 영국의 음악학자 엘리스(Ellis, Alexander John)에 의해 옥타브(1200cent)를 12등분하여 각 반음을 100cent로 균등하게 분할한 현재의 평균율이 도입되게 된 것이다. 다음은 각 음률의 진동수의 비율을 비교한 것이다. 음률은 약 53가지가 존재한다.
평균율과 순정율의 주파수차이
=========================================================================================================================
피타고라스 음계(Pythagoras Scale)
고대 그리스의 피타고라스가 창안한 음계로서 어떤 음을 기준음으로 하여 완전 5도씩 쌓아올린 다음 그 음들을 8도 아래로 전위시켜 파생된 음계이다. 수학적으로 정확하게 계산하여 정해진다 해서 순정율(pure temperament)라고도 하며, 국악의 삼분손익율과 음정의 진동비가 비슷하며 5도를 4번 쌓으면 그것이 곧 5음음계(pentatonic)가 된다. 그러나 피타고라스 음계는 5도로 쌓여지는 최후의 음 「 b#」음이 옥타브 C 음보다 24cent 높은 불합리한 음률이 된다. 이것을 피타고라스 코머(Pythagoras Comma)라고 하며 코머란 음정 사이에 존재하는 미세한 음정 차를 말한다.
삼분손익율(三分損益律)
어떤 길이의 관을 기본음으로 하여 그것을 세 등분한 뒤 그 2/3에 해당하는 부분이 완전5도가 되게 하고 이 완전 5도를 다시 세 등분한 것의 1/3을 보탬으로서 기본음으로부터 장2도 음(완전5도 음의 4도 아래)이 되게 하는 것으로 이러한 방법을 12번 거듭하면 12음을 얻게 된다. (12개 반음은 114cent와 90cent의 큰반음과 작은 반음이 혼재되어 있다)
'작편곡 이론' 카테고리의 다른 글
| [기본이론] 음표, 쉼표와 그 기보법 (0) | 2008.06.18 |
|---|---|
| [기본이론] 기본 교회선법, 조성과 조표 (0) | 2008.06.17 |
| [기본이론] 음자리표, 온음과 반음, 테트라코드 (0) | 2008.06.17 |
| [기본이론] 음이름, 창법, 보표 (0) | 2008.06.16 |
| 시작하며 (0) | 2007.10.30 |